In my preceding posts, I’ve described the dimensional levels of each facet of our “cubic” learning model: content, community, and context. This post (and the next several) will incorporate and build on content from those posts, so if you haven’t yet seen them, you might want to review them before continuing here.

In “cubic” learning, each element’s “dimensionality” increases as the learner becomes more engaged and plays a more central role. The increasing agency, skills, and responsibility learners must demonstrate at each progressive level also means that more and more, they need support rather than direction, individual resources rather than a one-size-fits-all recipe, and companions and partners rather than controllers. More dimensionality means more learner-centered — and learner-driven — learning.

As we’ve seen previously, the dimensional levels of the “cubic” model look like this, with the higher levels increasing the volume of the cube they generate:

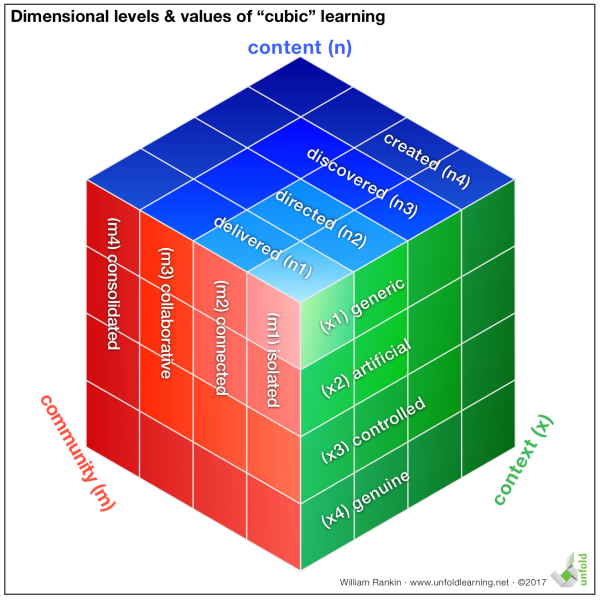
While “volume” in this model is something of a metaphor, it’s one backed up by research. For example, as both Anderson and Krathwohl’s revision of Bloom’s taxonomy and Webb’s “depth of knowledge” (DOK) argue, creating content not only requires more ability from learners than recalling, it also increases their learning potential: the deeper level of engagement makes learning more likely to take hold. In other words, moving from recall to creation increases the potential “volume” for learning — and therefore makes a bigger cube in this model.

This increase in learning potential as a learning approach increases in “dimensionality” mirrors decades of educational research. For example, in the “Learning and Transfer” chapter of the National Research Council’s How People Learn: Brain, Mind, Experience, and School (expanded edition: Bransford, Brown, and Cocking, eds, 2000), the editors summarize some of what researchers have discovered this way:

Learners of all ages are more motivated when they can see the usefulness of what they are learning and when they can use that information to do something that has an impact on others—especially their local community (McCombs, 1996; Pintrich and Schunk, 1996). Sixth graders in an inner-city school were asked to explain the highlights of their previous year in fifth grade to an anonymous interviewer, who asked them to describe anything that made them feel proud, successful, or creative (Barron et al., 1998). Students frequently mentioned projects that had strong social consequences, such as tutoring younger children, learning to make presentations to outside audiences, designing blueprints for playhouses that were to be built by professionals and then donated to preschool programs, and learning to work effectively in groups. Many of the activities mentioned by the students had involved a great deal of hard work on their part: for example, they had had to learn about geometry and architecture in order to get the chance to create blueprints for the playhouses, and they had had to explain their blueprints to a group of outside experts who held them to very high standards.” (61)

This isn’t just learning to pass a test, nor is it easy. What’s important for the learners this research describes is that their learning is meaningful — serving others in their community with projects that have a life in the real-world context outside of school.

The message is clear: dimensionality matters. It gives learners motivation to pursue learning, venues in which to demonstrate their learning, and an audience who helps them hone and refine their learning. Dimensionality moves learning from data and information toward knowledge and wisdom. Yet some approaches are inherently less dimensional — and have less potential to inspire deeper learning — than others. How can we determine which approaches have more potential, and how can we compare one approach with another?

One way to assess the learning potential of an approach is to map its defining characteristics onto each of the three facets — content, community, and context — and then multiply the associated numbers to get the overall volume of the shape that’s generated. We call this volume the “engagement and learning multiplier” (ELM). Approaches that feature low dimensionality generate small shapes while those with larger dimensions generate larger shapes. For example, an approach that delivers content (n1) to learners working largely in isolation (m1) in an artificial context (x2) would generate a correspondingly small volume and a small ELM:

1 · 1 · 2 = 2

An approach that features genuine creation by learners (n4) working in a highly collaborative way with others (m3) in a controlled “internship” context (x3) generates a much larger ELM:

4 · 3 · 3 = 36

Does this necessarily mean that the learner in the second approach will learn more? No. Learners can decide not to engage if they choose, no matter what learning approach they encounter. However, the second approach has a much higher potential for learning — and by its very nature, requires (and is more likely to generate) a higher level of engagement from the learners involved.

Approaches with high ELM scores have more going for them than just learning potential and engagement, however. For example, it’s also much harder to “fake” learning results in the second approach because it requires learners to demonstrate a higher level of internalization and expertise. In the model with the low ELM, learners can spend much of the learning time distracted or engaged in other activities. Since they’ll only be expected to repeat information that’s been delivered to them — and only in an artificial context, like answering essay questions about a case study — a quick bit of cramming can give them everything they need for success. They can answer the questions with a very superficial level of learning and understanding. On the other hand, the approach with the larger ELM requires learners who can think on their feet in a real-world (albeit, in this case, a controlled) setting. If they don’t have the knowledge, skills, and research and networking capabilities ready at-hand, they’ll have to work hard to get them — or they won’t succeed. They won’t be able to pretend and won’t be able to get by with a superficial level of learning because the project they have to create, delivered to a group with a certain level of expertise (including their peer learners) in a genuine context, will quickly collapse without real learning and real capabilities. It simply won’t be successful unless it encapsulates useful content productively for the community of people operating in that context.

Graphed, the possible ELM scores for various approaches look like this, with the lowest dimensional approaches (for example, approaches at level one on at least two facets — 1·1·x) scoring considerably less than higher dimensional approaches (such as those at level four on at least two facets — 4·4·x):

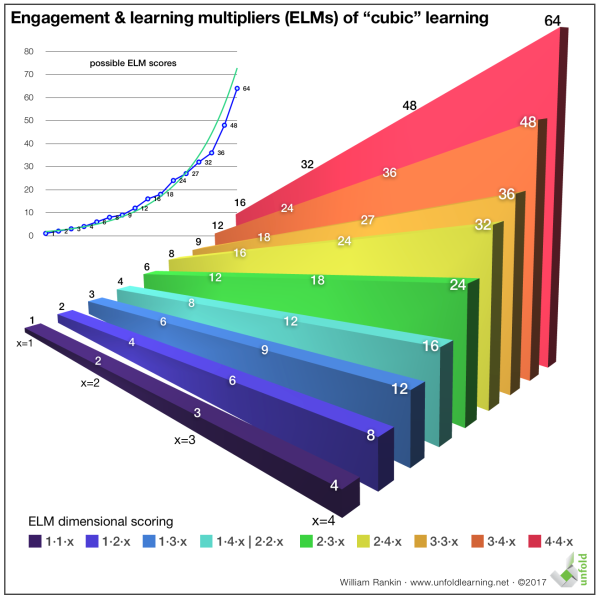
As you can see, the increase in ELM scores follows a geometric curve as one moves from approaches with low to high dimensionality. At the higher levels, increasing expectations of agency and expertise means learners have to demonstrate a more rigorous level of learning, but that learning is also significantly — even geometrically — more likely to stick with them.

However, this high expectation doesn’t necessarily mean learners must demonstrate a level of skill or knowledge only available to experts in a field. It means simply that they must demonstrate appropriately high capabilities relative to their developmental status. For example, nine-year-olds might gather stories and interviews to produce a video about the history of their town that’s played on a local television station. Or fifteen-year-olds might research local sustainable agricultural practices to design and plant a garden whose vegetables will be used in their school cafeteria. Both groups are working at high levels of dimensionality because they’re discovering and creating content empowered by rich collaboration in real-world contexts — and thus both approaches would have high ELMs.

If we think about learning volumetrically, considering the ELM scores of various approaches, we can begin to see why it might be useful to choose one approach over another, or to understand why one approach might produce richer or more comprehensive results than another. And thinking about their “cubic” value can give us an important tool not only for assessing what we’re already doing, but also for considering new approaches or new learning tools that we might encounter in the future. Will this new element change learning? We can have a better sense if we consider how it will impact the three dimensionalities.

When we apply the cubic model to a course — or any other learning enterprise — we can apply it to an individual day or activity, but to make a general assessment, we have to apply it to the way learning is typically conducted. A lecture course that features two days of team collaboration during an entire term isn’t really more dimensional; the collaboration is an anomaly — and its overall impact will likely be minimal. However, a lecture course that uses team collaboration every week as a way of situating and processing course material likely would be more dimensional. In this case, the collaboration is an integral part of the course’s construction and this would be reflected in a higher overall ELM score.

    *          *          *

As a guide for mapping “cubic” dimensions in your own context and assigning ELMs, the next several posts will assess some common learning approaches. We’ll look at graphical representations of the shapes they create and explore how — and why — they receive the ELM scores they have. I hope you’ll stay tuned!

You can find the first assessment — of a traditional lecture course — here.

 

 

 

©2017 William Rankin